มนุษย์รู้จักโน้ตดนตรีมายาวนาน มนุษย์ยุคโบราณมีการนำท่อกลวงเจาะรู และเส้นขึงตึงมาเป่าและดีดเป็นเครื่องดนตรีตั้งแต่สมัยก่อนประวัติศาสตร์ ต่อมาพีทาโกรัสเป็นคนแรกที่พบว่าโน้ตดนตรีสามารถหาจากความสัมพันธ์ทางคณิตศาสตร์ได้
การค้นพบความสัมพันธ์ระหว่างคณิตศาตร์และดนตรี
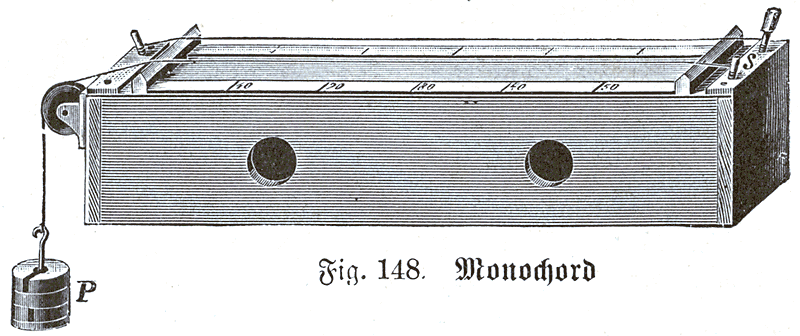
Monochord
อุปกรณ์ monochord ถูกประดิษฐ์ขึ้นมาเพื่อศึกษาเกี่ยวกับเสียง monochord จะมีที่เลื่อนคล้ายลิ่มอยู่ตรงปลาย และมีตุ้มถ่วงอยู่ด้านหนึ่งไว้ถ่วงเส้นลวดหรือเส้นใดๆ โดยมีหมุดยึดเส้นดังกล่าวอีกทางนึง เมื่อเลื่อนที่เลื่อนหรือเปลี่ยนตุ้มถ่วง เสียงที่เกิดขึ้นจะเปลี่ยนไป
Pythagorean Tuning
พีทาโกรัสอาศัยเส้นลวดบนอุปกรณ์ monochord พบว่าเมื่อแบ่งความยาวของเส้นลวดบน monochord เป็นสองส่วนเท่ากัน เสียงที่เกิดจากการดีดเส้นทั้งสองจะพ้องกันเป็นโน้ตเดียวกัน และมีอัตราส่วนเป็น 2:1 ของโน้ตแรก
เพิ่มเติม ที่เราทราบว่าเป็นโน้ตตัวเดียวกันเพราะเมื่อนำเส้นลวดยาวไม่เท่ากันหลายๆเส้นมาแบ่งครึ่งแล้วดีดตามลำดับจะได้ทำนองเดียวกันกับเส้นลวดที่ไม่ได้แบ่งครึ่ง

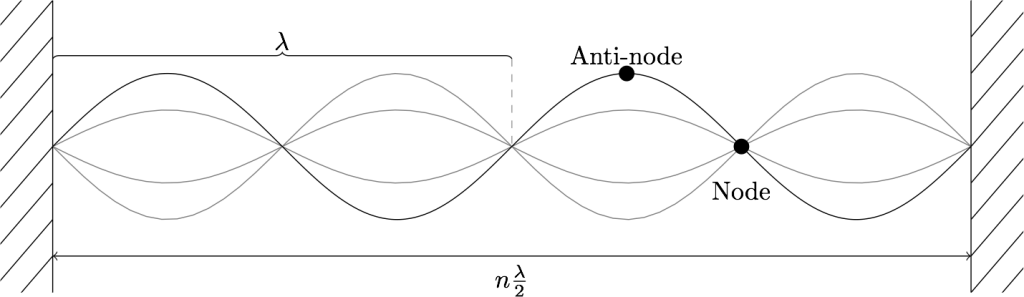
และถ้าแบ่งความยาวของเส้นลวดบน monochord เป็นสามส่วนเท่าๆกัน เสียงก็สั่นพ้องกันกับโน้ตแรกตามรูปด้านบน
ภาพ CC BY-SA 3.0
เพิ่มเติม เราสามารถทำการแบ่งเส้นลวดออกเป็น 1/3, 1/4, 1/5… ไปเรื่อยๆ เสียงก็ยังมีความสั่นพ้องกันแต่อาจลดระดับลงบ้าง

สรุปการค้นพบที่ได้จากการทดลองของพีธากอรัส
- เราจะทราบว่าเมื่อแบ่งเชือกเป็น n ส่วน เท่าๆกัน เสียงที่ได้จากการดีดพร้อมกับการดีดเส้นที่ไม่แบ่งจะกลมกลืนกันเสมอ
เพิ่มเติม ในฟิสิกส์เราทราบว่าเสียงที่ความถี่เป็น n เท่าจะฟังกลมกลืนกับเสียงความถี่ตั้งต้นเพราะทุกๆ n คลื่นจะซ้อนทับกับความถี่ตั้งต้นเสมอ
2. โน้ตที่กลมกลืนกับโน้ตตั้งต้นที่สุดคือโน้ตที่มีอัตราส่วน 2:1 และเป็นโน้ตเดียวกับโน้ตแรกแต่ระดับเสียงสูงกว่า
Pythagorean Tuning
พีธาโกรัสทดลองหาโน้ตจากการแบ่งเชือกออกเป็นสามส่วนเท่าๆกัน จนได้อัตราส่วน 3:2 อาศัยอัตราส่วนสองค่าคือ 2/1 และ 3/2 พีทาโกรัสจึงสร้างสเกลดนตรีอย่างง่ายได้ เรียกว่า
Pythagorean Scale
เนื่องจากเราทราบแล้วว่าถ้าเรามีโน้ตที่มีอัตราส่วนเป็น 3:2 โน้ตที่ได้จะให้เสียงที่กลมกล่อมกัน ดังนั้นถ้าเราคำนวณหาโน้ตจากอัตราส่วน 3:2 ไปเรื่อยๆเราจึงน่าจะได้โน้ตที่ฟังกลมกล่อมมากเพิ่มขึ้น
พีทาโกรัสจึงสร้างสเกลออกมาคือ
…, 1, 3/2, (3/2)^2, (3/2)^3, (3/2)^4, (3/2)^5, (3/2)^6 …
หรือ
…, 1, 3/2, 9/4, 27/8, 81/16, 243/32, 729/64…
อาจคำนวณกลับเป็น
…(2/3)^6, (2/3)^5, (2/3)^4, (2/3)^3, (2/3)^2, 1,…
ก็ได้
จากที่ทราบว่าทุกสองเท่าและครึ่งหนึ่งของอัตราส่วนคือโน้ตตัวเดียวกัน เมื่อแปลงอัตราส่วนให้อยู่ระหว่างอัตราส่วน 1 ถึง 2 แล้วเรียงลำดับจากค่าน้อยไปมากจะได้
1, 9/8, 81/64, 729/512, 3/2, 27/16, 243/128, 2
จากอัตราส่วนข้างบนจะเห็นว่า เมื่อเราเรียงโน้ตจากน้อยไปมากแล้ว โน้ตตัวที่สองไปจะมีระยะห่าง(Interval) จากโน้ตตัวแรกเป็น 9:8 ในขณะที่เมื่อคำนวณไปจนถึงโน้ตตัวที่ 6 และ 7 เราจะได้ระยะห่างใหม่เป็น 256:243 เมื่อวัดระยะห่างแต่ละโน้ตจะได้
ระยะห่างโน้ตเป็น
9/8, 9/8, 9/8, 256/243, 9/8, 9/8, 256/243
หรือ
whole, whole,whole, half, whole, whole, half
หากเราทำการคำนวณหาตัวโน้ตเพิ่มเป็น (3/2)^7, (3/2)^8, (3/2)^9… แล้วนำมาจัดให้อยู่ในอัตราส่วนระหว่าง 1 และ 2 จะได้
โน้ต 12 ตัว
1, 2187/2048, 9/8, 19683/16384, 81/64, 177147/131072, 729/512, 3/2, 6561/4096, 27/16, 59049/32768, 243/128, 2
มีระยะห่างเป็น
2187/2048, 256/243, 2187/2048, 256/243, 2187/2048, 256/243, 256/243, 2187/2048, 256/243, 2187/2048, 256/243, 256/243
มีครึ่งเสียงเป็น 256/243 และเต็มเสียงเป็น 2187/2048
เพิ่มเติม ในสมัยพีธาโกรัสนั้น เขาสร้างสเกล Pythagorean Scale ขึ้น แต่เขาไม่สอนลูกศิษย์ด้วยสเกล Pythagorean Scale แต่สอนสเกลดนตรีโบราณแทน
กำเนิด Tetrachord
ถ้าเรานำระยะห่างมาเรียงต่อกันเป็นรูปแบบต่างๆ เราจะพบว่า ต้องอาศัยโน้ต 4 ตัว เป็นจำนวนน้อยที่สุดที่จะทำให้เราใช้ระยะห่างครึ่งเสียงและเต็มเสียงได้มากกว่า 2 รูปแบบ
เพราะถ้าเราใช้ 1 โน้ตจะไม่เกิดโน้ตที่แตกต่างกัน ขณะที่ 2 โน้ตก็จะเรียงได้ 2 แบบคือ 9:8 และ 256:243 (ไม่สามารถใช้ระยะห่างทั้งครึ่งเสียงและเต็มเสียงได้) ส่วน 3 โน้ตจะได้ 9:8, 256:243 และ 256:243, 9:8 (เรียงได้เพียง 2 แบบเท่านั้น เมื่อนำไปใช้สร้างสเกลจะได้สเกล Pentatonic)
ระยะห่างโน้ตดนตรีไม่เท่ากัน
การเลือกโน้ตดนตรีด้วยการเพิ่ม/ลดโน้ตทีละ 3/2 เท่าทำให้เกิดระยะห่างเป็น
whole, whole,whole, half, whole, whole, half
และเป็นระยะห่างของ F lydian mode ในดนตรีสากลปัจจุบันนั่นเอง
ทำไมสเกลดนตรีถึงมี 12 โน้ต
เนื่องจากดนตรีปัจจุบันได้รับอิทธิพลจาก Pythagorean Scale ซึ่งเราจะพบว่าถ้าเราคำนวณหาโน้ตดนตรีมา 12 ตัวโน้ต เราจะได้โน้ตที่ 12 มีค่าเป็น (3/2)^12 = 129.75 ซึ่งมีค่าประมาณ 2^7 = 128 ดังนั้นโน้ต 12 ตัวจึงเป็นจำนวนแรกที่ทำให้สเกลดนตรี Pythagorean Scale มีค่าใกล้โน้ตแรกมากที่สุด
เพิ่มเติม เราสามารถคำนวณหาโน้ตต่อ จะได้สเกล 12 โน้ต และ 17 โน้ต หรือต่อไปได้เรื่อยๆ แต่การทำเครื่องดนตรีที่มีโน้ตดนตรีมากขนาดนั้นอาจใช้งานไม่สะดวก
ทำไมโน้ตดนตรีมี 7 ตัว
สเกลดนตรีของ Pythagoras สามารถประมาณได้ว่าทุกๆโน้ต 12 ตัว เสียงดนตรีจะวนมาโน้ตตัวเดิมอีกครั้ง ต่อมานักดนตรีพบว่า ถ้าเราต้องการให้นักดนตรีสามารถเปลี่ยนระดับเสียง ขึ้นและลงได้ทั้ง 12 โน้ต เราจะทำได้โดยใช้สเกลใหม่จาก สเกลโครมาติกเดิม เรียกว่าบันไดเสียงไดอาโทนิก (Diatonic Scale) คือ สเกลเมเจอร์ และสเกลไมเนอร์ โดยสเกลเมเจอร์มีโน้ต 7 ตัว และสเกลไมเนอร์มีโน้ต 7 ตัวเช่นกัน โดยระยะห่างระหว่างโน้ตทั้ง 7 ในสเกลเมเจอร์เป็น whole, whole, half, whole, whole, whole, half ส่วนบันไดเสียงไมเนอร์มีระยะห่างเป็น whole, half, whole, whole, half, whole, whole,
ทำไมโน้ตดนตรีเริ่มด้วย C และทำไมโน้ตดนตรี A เป็นลา
ใน European Music เมื่อ 600-1600 ปีก่อน นักดนตรีใช้ Mode ในการแต่งเพลง โดย Mode ทั้ง 4 มี Dorian, Phrygian, Lydian, Mixolydian และแต่ละ Mode การเพิ่มโน้ตลงไปโน้ตต่ำกว่าอีก 4 ตัว เรียกว่า Hypo-
ในสมัยนั้น Mode Dorain คือ Mode ที่มีเสียงต่ำสุด หมายความว่า ใน Mode Hypodorian จะมีโน้ตต่ำลงไปที่ตำแหน่งที่ 4 จากโน้ตแรกใน Mode Dorain
เมื่อเขียนตารางโน้ตจะได้ว่า แต่ละ Mode มีโน้ตเป็น
I – DORIAN: D E F G A B C D
II – HYPODORIAN: A B C D E F G A
III – PHRYGIAN: E F G A B C D E
IV – HYPOPHRYGIAN: B C D E F G A B
V – LYDIAN: F G A B C D E F
VI – HYPOLYDIAN: C D E F G A B C
VII – MIXOLYDIAN: G A B C D E F
VIII- HYPOMIXOLYDIAN: D E F G A B C
จะเห็นว่าใน Mode Dorain ถ้าเทียบกับโน้ตแรกในปัจจุบันคือ โน้ต D ซึ่งเมื่อนับลงไปอีก 4 ตำแหน่งจะได้โน้ต A ซึ่งคือเสียง ลา ในปัจจุบัน
ต่อมาเมื่อมีการใช้ระบบตัวอักษรแทนตัวโน้ต จึงกำหนดให้โน้ตต่ำสุดใน Mode คือ ลา เป็นตัว A นั่นเอง
ต่อมาบันไดเสียงเมเจอร์เป็นที่นิยมและโน้ตโดบนเปียโนสังเกตง่ายจึงใช้บันไดเสียง C Major เป็นหลัก
ต่อมาราว คศ. 1000 มีการเพิ่มโน้ต F# และ Bb ลงไปใน Mode เพื่อแก้ปัญหา Tritone เมื่อนำมาเพิ่มใน Mode จะได้
Dorian เพื่ม Bb = D aeolian
Phrygian เพิ่ม F# = E aeolian
Lydian เพิ่ม Bb = F major
Mixolydian เพิ่ม F# = G major
ต่อมาในปี คศ.1549 เมื่อมีคนรู้จักสเกลเมเจอร์ พบว่า C Major ไม่มีชาร์ป แฟลท การใช้โน้ตโด เป็นโน้ตแรกในการเรียนสเกลดนตรีจึงแพร่หลาย เพราะการหาโน้ตโด บนเปียโนง่ายดาย
สเกลดนตรีธรรมชาติ (Harmonic)
ตามที่กล่าวแล้วว่าทุกๆฮาร์โมนิคคี่จะเกิดเสียงใหม่ หากเรานำโน้ตใหม่นั้นมาเรียงเป็นสเกลจะได้บันไดเสียงธรรมชาติขึ้น
เช่นโน้ต 7 ตัวเป็น
1:1 | 9:8 | 5:4 | 21:16 | 3:2 | 27:16 | 15:8 | 2:1 |
สเกลแบบแบ่งเท่า (Equal Tempered Scale)
ทั้งสองสเกลข้างต้นไม่สามารถทำการเปลี่ยนสเกลขึ้นลงได้อิสระ เพราะเมื่อทำการเปลี่ยนสเกลจะมีระยะห่างที่ผิดไป ทางออกของเครื่องดนตรีแบบ Fixed Pitch Instrument จึงปรับตั้งเสียงดนตรีให้ห่างเท่ากัน ให้ผลน่าพอใจระดับหนึ่งเพราะระยะห่างไม่ต่างจากสเกลทั้งสองมากนัก แต่ยังให้เสียงที่แยกไม่ออกง่ายๆ
ที่มา https://en.wikipedia.org/wiki/Pythagorean_tuning
https://en.m.wikipedia.org/wiki/Just_intonation
https://en.wikipedia.org/wiki/Harmonic_series_(music)
https://en.wikipedia.org/wiki/Equal_temperament
https://www.quora.com/Why-does-the-music-scale-start-on-C-instead-of-A?ch=10&share=df7e8d8e&srid=WQA5r